Widerstände

Widerstände haben wir schon in unserem Wassermodell kennengelernt, wo sie weniger Wasser fliessen lassen, weil sie dem Wasserfluss einen Widerstand entgegensetzen. Bei den elektrischen Widerständen ist es genauso: es fliessen weniger Elektronen pro Zeit durch die Leitung als ohne Widerstand, der elektrische Strom ist schwächer.

Aber wozu will man denn einenWiderstand? Sollen nicht am besten so viele Elektronen wie möglich fliessen?

Nicht immer! In unserer Schaltung vertragen die Leuchtdioden nur ca. 30mA an Strom. Mehr und sie würden durchbrennen. Der Widerstand verhindert das. Schon sinnvoll.

Wir messen Spannung und Strom an Diode, Leuchtdiode, Glühlämpchen und Widerstand bei verschiedenen Betriebsspannungen.

Wir schreiben das natürlich wieder auf. Wie? Genau, in einer Tabelle!

Spannung/V	Strom/mA	Beobachtung
0	xxx	dunkel
1	xxx	dunkel
2	xxx	dunkel
3	xxx	beginnt zu leuchten
4	xxx	xxx
5	xxx	xxx
6	xxx	xxx
7	xxx	xxx
8	xxx	xxx
9	xxx	xxx

Dabei machen die Gruppen folgendes:

Reißnägel: grüne LED
Manhatten: rote LED
Breadboard: Glühlampe
Simulierer: Widerstand und Diode 1N4148 (ja, mehr Arbeit, aber ihr habt ja auch mehr Messgeräte)

Gibt es dabei ein Problem? Welches?
Wir haben nicht genug Messgeräte um Spannung und Strom gleichzeitig zu messen. Wie lösen die Kinder das?

Eine gute Lösung ist Teamwork: zwei Gruppen teilen sich die DMMs und erst misst eine, dann die andere. Wir schreiben das auf, das könnte auch später hilfreich sein.

Jetzt liest jede Gruppe ihre Werte vor

Macht das Sinn? Können wir uns unter den vorgelesenen Werten etwas vorstellen? Gibt es Unterschiede zwischen den Gruppen? Können wir daraus etwas lernen?

Das Diagram

Nicht wirklich, oder? Daher lernen wir jetzt eine neue Methode kennen, so viele Werte(paare) dazustellen und mental zu verarbeiten.

Jede Gruppe holt sich ein Blatt Millimeterpapier

Die Betreuer helfen euch hier:
Die dicken Linien sind jeden Zentimeter, die dünnen jeden Millimeter (drum heisst es Millimeterpapier). Wir zeichnen ein Koordinatensystem: nach rechts die "unabhängige Variable" (das ist die, die wir geändert haben, also in diesem Fall die Spannung. Wir nennen das die X-Achse) und nach oben die abhängige Variable (bei uns also der Strom, wir nennen das die Y-Achse). Da wo sich beide Achsen treffen, ist der Nullpunkt.

Jetzt müssen wir festlegen, wieviele Kästchen 1 Volt sein sollen. Das kann z.B. 1 Kästchen (1 cm) sein. Dann schreiben wir jeweils nach 1 cm die Zahlen 1, 2, 3, 4, ... an die X-Achse.

Genauso machen wir es mit der Y-Achse. Wir wählen z.B. 1 cm als 10 mA. Oder als 1 mA. Wir sollen mit unseren Werten möglichst das ganze Blatt beschreiben.

Jede Gruppe zeichnet die Punkte der Messwerte auf das Millimeterpapier

Wie werden wohl die Wertepaare für die Werte zwischen den Punkten sein?

Wir können einfach mehr Messungen machen, wenn wir uns unsicher sind, oder mit viel Gefühl eine durchgehende Kurve zwischen den Messwerten einzeichnen. Es geht einfach zwischen den Messwerten so weiter, wie davor und danach. Wenn wir irgend etwas "Wildes" vermuten, dann sollten in diesem Bereich nochmal messen.

Jede Gruppe zeichnet den Graphen der Messwerte auf das Millimeterpapier und verbindet die Punkte

Für den Widerstand mit 2.2k sieht das für die Simulaten dann etwa so aus:

Wir schreiben noch auf das Blatt, was wir gemessen haben (z.B den Widerstand mit 2.2k) und wir geben den Achsen eine Beschriftung, z.B. für die Y-Achse I / mA und die X-Achse U / V.

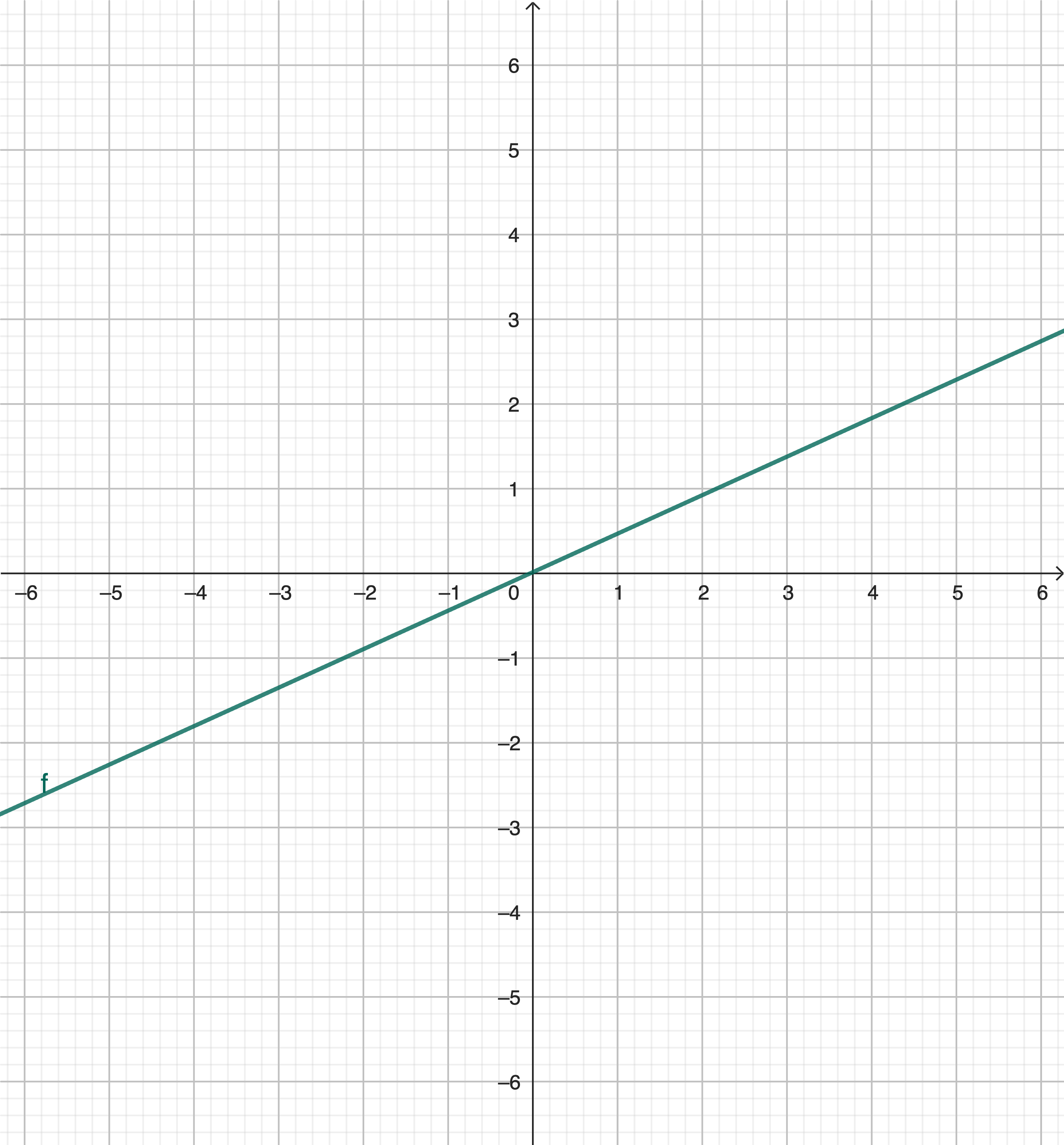
Mithilfe des Diagramms können wir jetzt viel besser verstehen, wie der Widerstand funktioniert: je mehr Spannung ich am Widerstand habe, umso mehr Strom fliesst. Und zwar fliesst bei der doppelten Spannung der doppelte Strom. Dieses Diagramm nennt man eine Kennlinie.

Jede Gruppe schaut sich das Diagramm genau an, um es zu verstehen

Die Kurve hat eine gewisse Steigung. Das ist, wie steil sie ist, genau wie bei einem Berg, auf den ihr kraxelt. Die Steigung ist ein Maß für die Leitfähigkeit des Widerstands: je steiler die Kurve ist, umso mehr Strom fliesst bei gleicher Spannung, der Widerstand leitet also mehr (besser). Die Steigung S = Y / X .

Jede Gruppe rechnet die Steigung für unterschiedliche X-Werte (Spannung) aus.

Wir bekommen imm den gleichen Wert für die Steigung (Leitfähigkeit). Der Wert hängt also nicht von Spannung oder Strom ab. Es ist eine Eigenschaft des Widerstands.

Anstatt der Leitfähigkeit S arbeiten die Elektroniker lieber mit dem Widerstand. Das ist der Kehrwert: R = 1 / S . Oder auch R = X / Y .

Jede Gruppe rechnet den Widerstand für verschiedene Spannungen aus

Wir verwenden dazu gerne den Taschenrechner im Handy. Wir erhalten immer den gleichen Wert: 2200 Ohm oder 2.2 kilo-Ohm.

Ohm'sches Gesetz

Georg Simon Ohm war ein .... PHYSIKER (was sonst) und er hat als erster diesen Zusammenhang erkannt. Ihr seht also, um ein großer Physiker zu sein, muss man gar nichts super Schweres machen, man muss nur genau hinschauen.

Nach ihm ist das Ohm'sche Gesetz benannt und es ist das wichtigste Gesetz in der Elektronik. Wenn ihr euch vom heutigen Tag nur das merkt, dann war dieser Tag schon ein voller Erfolg!

Ohm'sches Gesetz: R = U / I
U = R * I
I = U / R

Nicht wirklich schwer, oder?

Farbcode

Der Widerstandswert ist die definierende Eigenschaft eines Widerstand und daher super wichtig. Da die Widerstände so klein sind und in verschiedener Orientierung eingebaut werden, haben die Elektroniker beschlossen, dass sie den Widerstandswert nicht als Zahlen auf den Widerstand drucken, sondern ihm Farbringe geben. Diese Ringe liest man wie folgt:

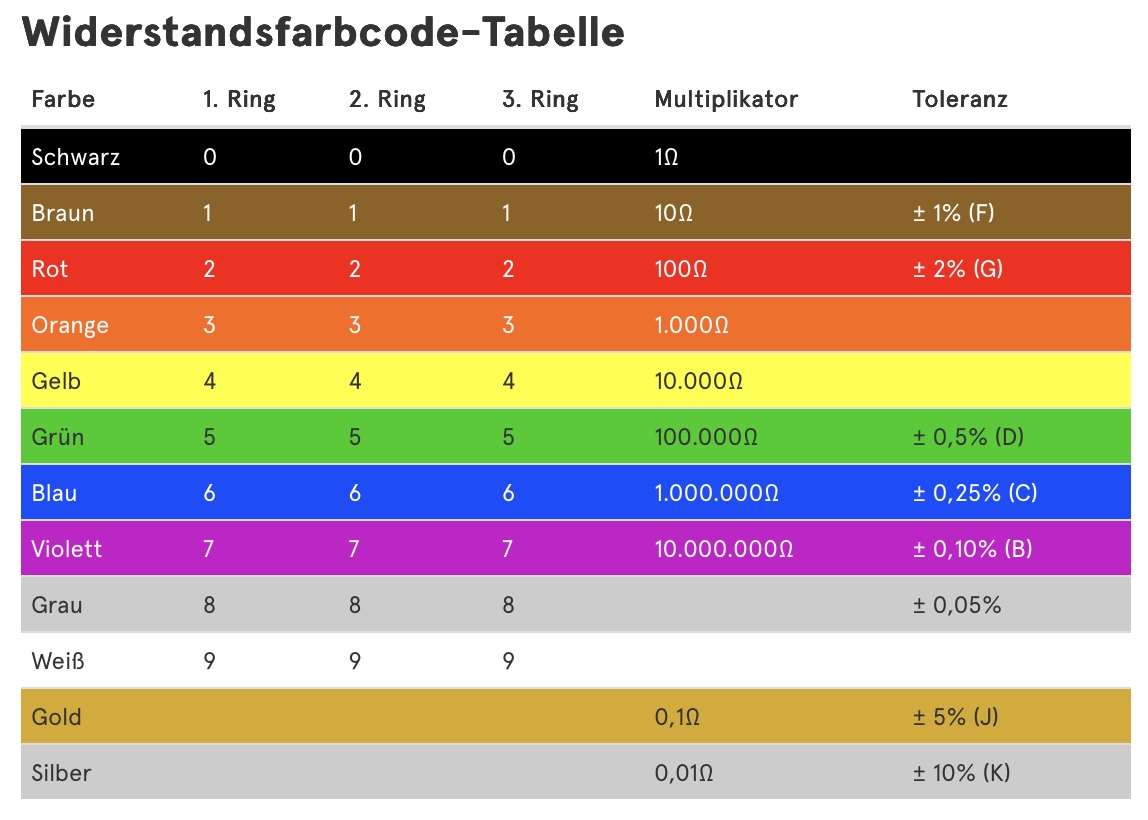
Bei Widerständen mit 4 Ringen: der erste Ring ist der am nächsten zu einem Ende des Widerstands. Dabei zählen nur die Farben ausser Gold und Silber. Die ersten beiden Ringe geben den Wert an, der dritte Ring gibt den Multiplikator (x10, x100, x1000, etc.).

Der vierte und letzte Ring gibt die Toleranz an, wie genau der tatsächliche Wert dem aufgedruckten entspricht. Man kann die Widerstände in der Fabrik nämlich nicht ganz genau herstellen, daher haben sie immer eine gewisse "Toleranz". 10 % (Silber) sind meistens gut genug, aber für ganz genaue Anwendungen (etwa wenn man ein Messgerät baut) braucht man ganz genaue Widerstände. Die gibt es zu kaufen, sie sind aber deutlich teuerer.

Bei Widerständen mit 5 Ringen: der erste Ring ist der am nächsten zu einem Ende des Widerstands. Dabei zählen nur die Farben ausser Gold und Silber. Die ersten drei Ringe geben den Wert an, der vierte Ring gibt den Multiplikator (x10, x100, x1000, etc.) und der fünfte Ring die Toleranz. Diese Widerstände haben eine wesentlich kleinere Toleranz (sind also besser), aber meistens brauchen wir keine so genauen Widerstände.

SMD Widerstände

Heute gibt es auch ganz kleine Widerstände, die nicht rund (zylinderförmig) sondern rechteckig (quaderförmig) sind. Da ist man von den Farbringen wieder abgekommen und druckt statt dessen den Wert auf eine Seite. Da man aber nicht viel Platz hat, nimmt man wieder das System mit den Multiplikatoren.

Ein Beispiel könnte so aussehen: 222
Die ersten beiden Ziffern geben den Wert, also 22.
Die dritte Zahl ist der Multiplikator, also x100 (hat 2 Nuller)
Es sind also 22 x 100 = 2200 Ohm, unser bekannter 2.2k Widerstand!

Ein anderes Beispiel könnte so aussehen: 103
Die ersten beiden Ziffern geben den Wert, also 10.
Die dritte Zahl ist der Multiplikator, also x1000 (hat 3 Nuller)
Es sind also 10 x 1000 = 10000 Ohm, ein 10k Widerstand!

Auch hier gibt es Widerstände mit 4 Ziffern, die dann wie die Farbcodes mit 5 Ringen gelesen werden.

E12 Reihe

Warum haben jetzt die Widerstände meistens so krumme Werte? 2.2k statt 2k?

In der Anfangszeit hatte man tatsächlich 2k und 3k und so weiter. Aber man merkte dann, dass ein Widerstand von 8k mit 10 % Toleranz 8k - 800 Ohm = 7200 Ohm bis 8k + 800 Ohm = 8.8k haben kann, ein Widerstand von 9k aber 9k - 900 Ohm = 8.1k bis 9k + 900 Ohm = 9.9k haben kann. Wie man sieht, überlappen die beiden Bereiche und das fand man nicht gut, weil ein Widerstand mit 8.5k sowohl als 8k als auch als 9k bedruckt sein kann. Verwirrend.

Daher legte man (speziell für Widerstände mit 10 % Toleranz) fest, dass es zwölf Werte pro Dekade (z. B. 1 bis 10, 10 bis 100 usw.) geben soll. Daher heisst diese Reihe E12 (es gibt auch die E24 Reihe, die dann z.B. 24 Werte pro Dekade hat). Die E12-Reihe umfasst folgende Werte pro Dekade: 1, 1.2, 1.5, 1.8, 2.2, 2.7, 3.3, 3.9, 4.7, 5.6, 6.8, 8.2. Wie man sieht, ist der Abstand zwischen zwei Werten am Anfang klein und am Ende groß.

Wenn wir jetzt einen Widerstand mit 6.8k und 10% Toleranz betrachten, so kann er 6.8k - 680 Ohm = 6120 Ohm bis 6.8k + 680 Ohm = 7480 Ohm haben.
Und der 8.2k hat 8.2k - 820 Ohm = 7380 Ohm bis 8.2k + 820 Ohm = 9020 Ohm.
Der überlappende Bereich ist jetzt viel viel kleiner und damit kann man leben. Probiert es gerne mal für andere Werte aus!

Vorsilben

Wir haben schon gesehen, dass der Strom in Ampere gemessen wird. Aber oft sind unsere Ströme viel kleiner und anstatt ganz viele Nullen zu schreiben, verwenden wir Vorsilben (Präfixe). Wir verwenden also mA (milli-Ampere) statt Ampere. Ein milli-Ampere ist 1 / 1000 Ampere. Neben milli gibt es noch viele andere Vorsilben:

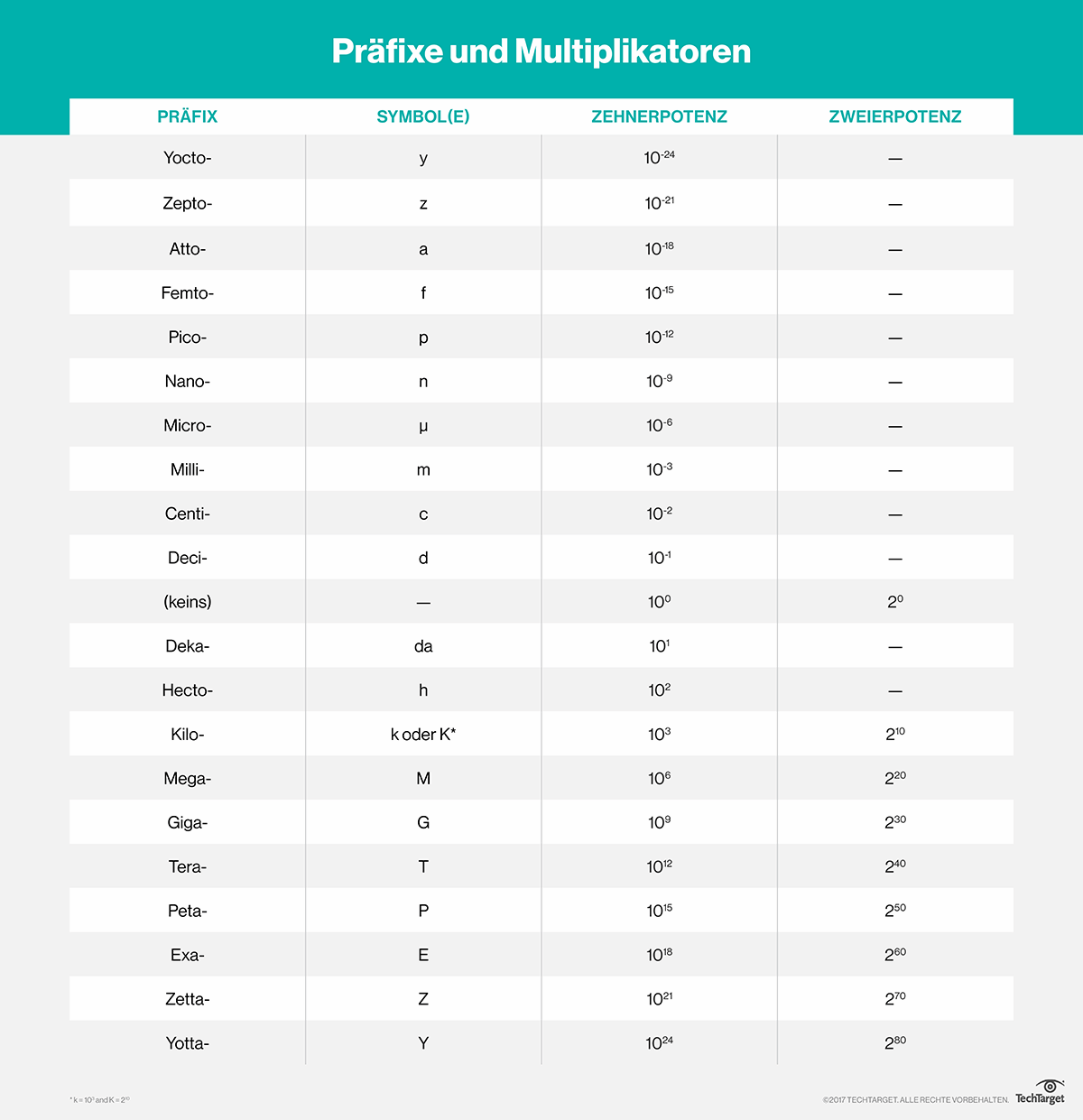
Wir brauchen uns nur diese sechs zu merken:
pico = 10^-12, nano = 10^-9, mikro = 1 / 1000000, milli = 1/1000, kilo = 1000, mega = Million

Widerstandsmessgerät

Weil die Widerstände so wichtig sind, hat unser DMM einen extra Messbereich für Widerstände. Die Betreuer zeigen euch, wie man den einstellt. Das ist praktisch, wenn man mal nicht sicher ist, welchen Wert ein Widerstand hat, oder wenn man meint, ein Widerstand könnte defekt sein (auch das kommt vor!).

Wenn man einen Widerstand misst, dann muss er von allen anderen Spannungsquellen getrennt sein und es darf auch sonst nichts angeschlossen sein. Und auch wenn man den Widerstandsbereich einstellt, muss das Messgerät von der Schaltung getrennt sein.

Was passiert, wenn ihr die Prüfspitzen im Widerstandsbereich mit den Händen anfasst? Was, wenn ihr die Finger feucht macht (anlecken)?

Auch euer Körper hat einen Widerstand und der ist garnicht so groß. Mit feuchten Fingern sind es ein paar kilo-Ohm. Daher nehmt ihr zum Anschliessen eines Widerstand die Kroko-Bandl und nicht eure Finger!

Wir probieren aus, wie sich der angezeigte Widerstand ändert, wenn wir ihn mit den Fingern statt mit den Kroko-Bandln halten

Piepser

Oft will man nur wissen, ob eine bestimmte Verbindung besteht und nicht, wie groß der Widerstand ist. Gerade wenn man dann nicht auf das Messgerät schauen kann, weil man die Prüfspitzen wo hinhalten muss, ist es praktisch, wenn das Messgerät piepst, wenn Verbindung besteht. Die DMMs haben alle auch so einen Piepser eingebaut. Die Betreuer zeigen euch, wo.

Im Piepser-Bereich die Prüfspitzen kurzschliessen

Wir können jetzt mit dem Ohmmeter oder dem Piepser verschiedene Gegenstände auf Leitfähigkeit (Widerstand) prüfen.

Reihenschaltung

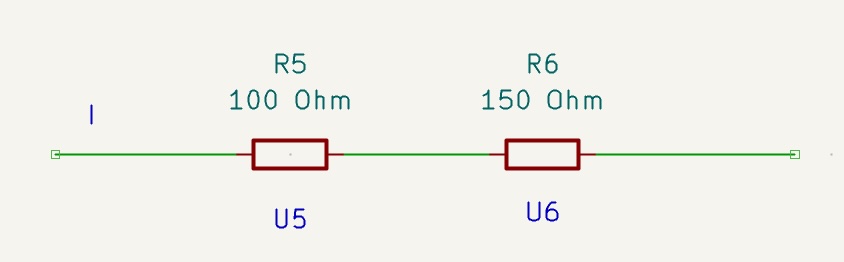
Wenn der Strom nacheinander durch zwei Widerstände (oder allgemein Bauteile: Glühlämpchen verwenden!) fliessen muss, dann sprechen wir von einer Reihenschaltung. Da der Strom nirgends "aus kann" (weil es keine Abzweigungen gibt), muss der gleiche Strom I durch beide Widerstände fliessen.

Mit dem Ohm'schen Gesetz können wir jetzt leicht die Spannungen über den Widerständen R5 bzw. R6 ausrechnen:

U5 = I * R5

U6 = I * R6

Wir bauen die Reihenschaltung mit zwei beliebigen Widerständen auf und messen Strom, Gesamtspannung und die Teilspannungen U5 und U6. Stimmt es mit der Rechnung überein?

Der Gesamtwiderstand ergibt sich auch aus dem Ohm'schen Gesetz:

R_gesamt = (U5 + U6) / I

Wir setzen die Teilspannungen von oben ein:

R_gesamt = (I * R5 + I * R6) / I

Wir können den Strom I ausklammern und dann wegkürzen:

R_gesamt = I * (R5 + R6) / I

R_gesamt = R5 + R6

Bei einer Reihenschaltung von Widerständen können wir die Werte der Widerstände einfach addieren!

Wir messen die Reihenschaltung mit dem Ohm-Meter. Stimmt es mit der Rechnung überein?

Parallelschaltung

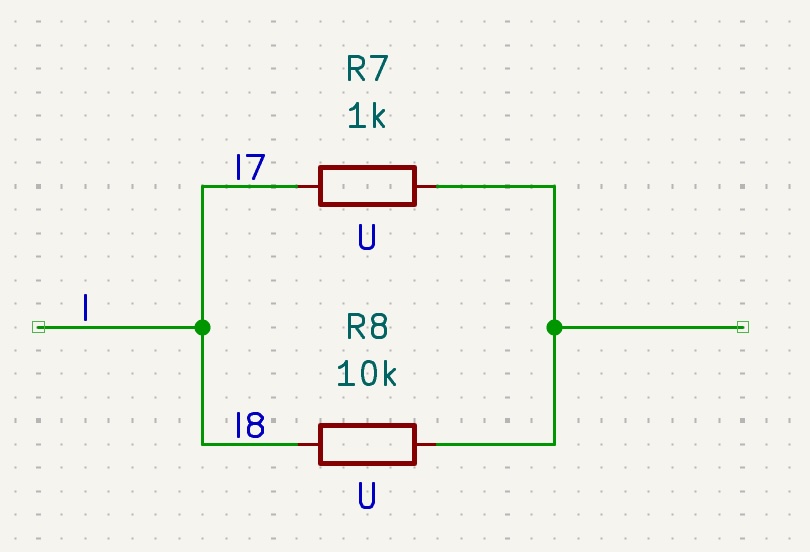
Wenn zwei (oder mehr) Widerstände (oder allgemein Bauteile: Glühlämpchen verwenden!) parallel geschaltet sind, dann liegt an beiden die gleiche Spannung U an. Wir sprechen von einer Parallelschaltung.

Mit dem Ohm'schen Gesetz können wir jetzt leicht die (Teil-)Ströme durch die Widerstände R7 bzw. R8 ausrechnen:

I7 = U / R7

I8 = U / R8

Wir bauen die Parallelschaltung mit zwei beliebigen Widerständen auf und messen Ströme I=I_gesamt, I7, I8 und die Spannung U. Stimmt es mit der Rechnung überein?

Der Gesamtwiderstand ergibt sich auch aus dem Ohm'schen Gesetz:

R_gesamt = U / I_gesamt

Der Gesamtstrom I ergibt sich als die Summe der Teilstöme, das werden wir im nächsten Kapitel etwas genauer anschauen:

I_gesamt = I7 + I8

Wir setzen die Teilströme von oben ein:

R_gesamt = U / I_gesamt = U / (U / R7 + U / R8)

Wir klammern jetzt im Nenner (unten) U aus und kürzen es weg:

R_gesamt = U / (U / (1 / R7 + 1 / R8)) = 1 / ( 1 / R7 + 1 / R8))

Das sieht man klarer, wenn man es mit Bruchstrichen schreibt:

	1
R_gesamt =
	(1 / R7 + 1 / R8)

Wir messen die Parallelschaltung mit dem Ohm-Meter. Stimmt es mit der Rechnung überein?

Zurück